📕 Node [[20210116145100 act4e_session_1_transmutation]]
📄 20210116145100-act4e_session_1_transmutation.md by @ryan
ACT4E - Session 1 - Transmutation
tags : [[category theory]]
source : ACT4E - Session 1 - Transmutation on Vimeo
Notes
- An arrow describes a transmute, a thing that transforms resources from one to another
- \(X \to Y\) means transforming X into Y
- Transformations can be composed, \(X \to Y \to Z\), so for all intents and purposes, \(X \to Z\)
-
An (A,B)-process (\(P(A,B)\)) consists of:
- A set S, element’s of which are called states
- An update function: \(f: A \times S \to S\)
- A readout function: \(f: S \to B\), where, given a certain state, will give you a certain output
-
Given two processes, we can compose a system \(P(A,C)\) such that:
- \(A \to P(A,B) \to B \to P(B,C) \to C\)
- At a certain abstraction, all these things are the same
- What makes them the same is composition, transformations, resources, etc.
-
A category \(C\) is defined by four constituents:
- Objects: a collection \(Ob_c\) whose elements are called objects
-
Morphisms: For every pair of objects \(X, Y \in Ob_c\), there is a set \(Hom_c(X,Y)\), the elements of which are called morphisms from X to Y
- morphisms are like functions, or “arrows”
- Identity morphisms: for each object X, there is an element \(id_x \in Hom_c(X,X)\) which is called the identity morphism of X
- Composition operations: given any morphism \(f \in Hom_c(X,Y)\) and any morphism \(g \in Hom_c(Y,Z)\), there exists a morphism \(f \circ g\) in \(Hom_c(X,Z)\) which is the composition of f and g
-
Categories must also satisfy the following conditions:
- Unitality: for any morphism \(f \in Hom_c(X,Y): id_x \circ f = f \circ id_y\)
- Associativity: for \(f \in Hom_c(X,Y), g \in Hom_c(Y,Z), h \in Hom_c(Z,W): ( f \circ g ) \circ h = f \circ ( g \circ h )\)
- Many morphisms can exist between objects
-
Examples:
-
A currency category could have:
- Objects: a collection of currencies
- Morphisms: currency exchanges
- Identity morphism: 1 USD = 1 USD
- Composition of morphisms: Could convert from USD -> CHD -> EURO
-
A currency category could have:
- a subset of a category
- \(X -> Y\) and \(Y -> X\) are opposite categories of one another
Backlinks
- [[category]]
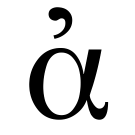
Rendering context...