Thank you for visiting the Agora of Flancia!
This Agora is in active development. Please report bugs and send feedback!
Settings
Auto-expand Settings
Auto-pull Settings
Display Settings
Browse Agora as
If you notice any strangeness, try clearing your local storage or reach out for support at agora@flancia.org.
Joining this Agora
To learn how to contribute, please open the Join panel.
Joining this Agora
For now, some work is required 😇With your digital garden
Enter your details to join immediately!
Or send email to signup@anagora.org with the following information:
- The URL of a Git repository containing your digital garden, wiki or blog; or of the content you would like to contribute.
- Your desired username (you can check for existing users here).
Please also reach out if you are interested in joining but need clarification or assistance. We are working on making this process less manual and more user friendly and inclusive :) Thank you for your patience!
From social media or chat
You can contribute:
This you find in the Agora of Flancia…
x
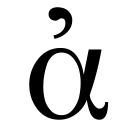
Loading Agora node...